Area of a Triangle

With all this talk about triangles and their side lengths and angles, we shouldn't forget to discuss how to find the AREA of a triangle.

You are probably familiar with one formula for finding the area of a triangle:

Area = 1/2 (base)(height)

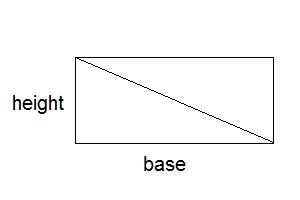
Compare this to finding the area of a rectangle:

The area of the rectangle is equal to the product of (base) x (height)..... (or length x width). However, by drawing a diagonal within the rectangle which joins two opposite corners, you can see that each newl! y-formed triangle is equal to half of the area of the original rectangle. Therefore, the area of a triangle is one-half the area of the rectangle, as shown by this triangle area formula. Even if you are looking at a triangle that doesn't immediately look like it is half of a rectangle, this formula still applies.

To prove it, you can draw a line in to represent the height, as I have shown here, thus creating two smaller triangles, and you can rearrange them to see that they indeed are equal to the area of half a rectangle:

That is one way to find the area of a triangle. However, if instead of base and height measurements, you are given lengths of sides or angles, this method won't work for you. In this case, you need to use a trig equation to solve for the area of a triangle.

Let's start w! ith the first equation we had above, and modify it. By the standard trig identities, we can show that:

height = (a)(SinC)

So substituting that into our formula:

Area = 1/2(base)(height)
Area = 1/2(b)(a)(SinC)

And this is the trig formula for solving the area of a triangle!

Area = (1/2)abSinC

You can use this to find the area of a triangle where you know any two sides and the angle between them! It's that easy!

Area of a triangle formula